今朝は早起きできた。
SDカードの挿抜時に電圧降下が起きるという話がChaN氏のサイトに書いてあったので、今いじくっているラズパイピコの基板の電源回路を調整した。対策がない場合にどれくらい良くないのかは測定していないが、まああのうっすい基板に付いてる部品ではほとんどエネルギーの保持力はないだろう。
ラズパイ側に100uFのコンデンサ、SDとの間に330uHのインダクタ、SD側に10uFのコンデンサを付けた。動揺波形はこんな感じ。
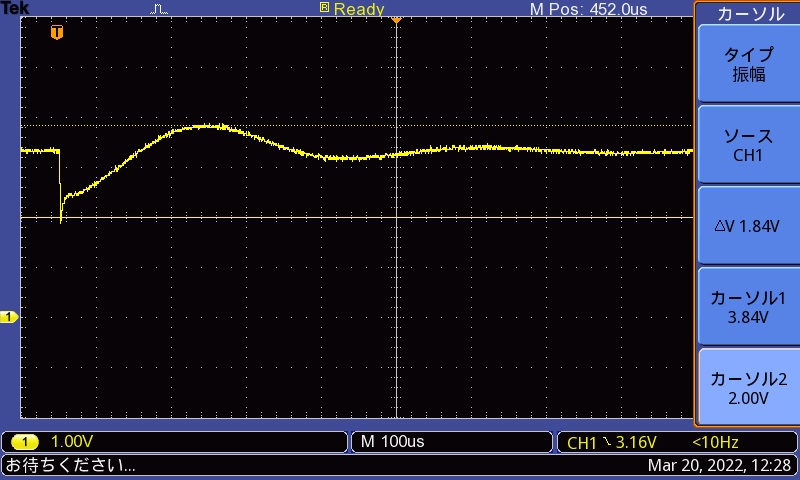
うーーん、もうちょっと安定してくれると思ったのだが。1.3Vくらい下がった後で戻るのに100usくらいかかっている。まあラズパイの方はリセットかかったりしてないようなので良いか。
そういえばこの波形はSDカード側で測っていた。よく考えたらインダクタを挟んだラズパイ側で測るべきだった。明日はそっちを測ってみるか。100uFついてんだからこっちよりかまともな波形だろう。
今日解いた競プロの問題。
ARC137-A 自力AC。適当に感覚でAC出来るかと思ったが無理だったので、ちゃんと考えたらACした。最初からちゃんと考えればよかった。
xとyを軸に取った二次元空間を考えて、条件を満たすxとyを考えると三角形になることが分かる。y-xが大きい方から順に調べていけば、gcd(x,y)=1なる点はそこそこの密度で分布しているはずなのでいずれぶちあたる。密度の証明はまあクソむずいんだろうがそこはまあこの程度の制約ならなんとなくで十分だろう。
ARC133-B 自力AC。めちゃめちゃきつかった。
時間・空間O(N^2)のDPはすぐに書けたがそれのオーダーを落とす手立てがなかなか思い浮かばず、最終的に絶対想定解じゃないよなと思いつつ双対セグ木を持ち出してACした。想定解はLISらしい。まだ理解できてない。
ARC134-C 自力AC。かなり悩んだが、一度思いついたら簡単だった。
それぞれの箱に入っている1でないボールの数をそれぞれ$g_1, g_2, … g_K$とすると、最低限必要な1のボールの数は$(g_1+1)+(g_2+1)+…(g_K+1)=\sum g_i + K$になる。$\sum g_i$の値は一定なので、べつに1でないボールをどう入れようが必要になる1のボールの数は変わらない。1でないボールを好きに割り振り、1のボールをそれぞれの箱に最低限配布して余った1のボールをまた好きに割り振ればいいだけだ。
ここで、ボールの割り振り方は$_kH_{a_i}$になるわけだが、$a_i$がいかんせんでかい。どうしたものかと思ったが、Kが小さいのでこれが活用できそうだった。定義に立ち帰って計算してみると$_kH_{a_i}=_{k+a_i-1}C_{a_i}=\frac{(k+a_i-1)!}{(a_i)!(k-1)!}$である。$\frac{(k+a_i-1)!}{(a_i)!}$はO(K)で計算できる。これでめでたく各$O(K)$、全体$O(NK)$で計算出来た。
ARC135-C 自力AC。ちゃんと実験したら意外と解けた。
これは数式をこねてみると分かるが、結局のところどう操作しても$A_1\oplus A_i, A_2\oplus A_i, … A_N \plus A_i$の形にしかならない。つまりN通り+何も操作していない場合の1通りしかありえる値は存在しない。
N通りの場合を高速に算出するのも多少頭を使ったが、bitごとに分けて各bitの1と0の数の挙動を考えればそう難しくはなく、全体$O(N\log(\max A_i))$で数えられる。
ラズパイピコの環境構築の話をlablogに書いた。純Windowsでの環境構築はあきらめた。
結局この記事にかなりの時間を費やしてしまった。CMake?はこの不具合なんとかしてほしい。自分はこの不具合の原因がCMakeなのかpico-sdkなのかすらよく判定付かないのでうかつにissueも建てられない。
CMakeと格闘していたらこういう知識を仕入れた。へ~。
https://oshiete.goo.ne.jp/qa/1246439.html
Categories: 未分類