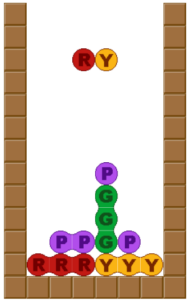
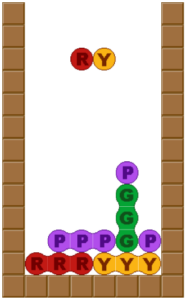
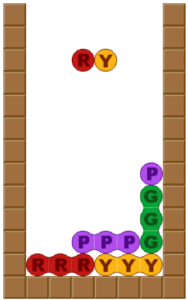
溜まってたタスクで1つでかいの終わらせた。
とっておいたアイスを食べた。
とっておいた菓子パンを食べた。
飼っていたメダカの最後の一匹が往生した。
俺は無敵だ。
電気イルカさんの記事を読み漁って、ぷよぷよの中央不定の気持ちがちょっとだけ分かってきた。まあ前に読んだあまたんさんの記事と同じことを書いているようなものになるのだが、自分の言葉で説明できそうな感じに飲み込めてきたので嬉しくなって書く。
基本の発想はこれ。

ダブル 
2連鎖 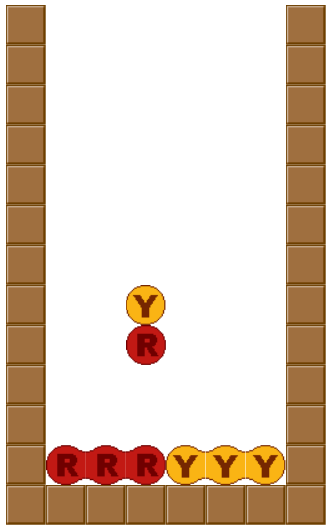
2連鎖
この上下の間の空間に3連鎖を作ることで、4Wか5連鎖が狙える。どうにかしてこの上下を隔離して、最後にくっつくように仕向ける。
で、隔離するための第一の発想がこれ。

これでとにかく隔離できる。隔離さえ出来ていればいいので、上の赤黄ぷよはどこに置いてもいい。どこに置くにしろ、間のぷよによる連鎖が終わった後で落ちてきてくっつくという結果は得られるのでどこに置いても同じ結果が得られる。
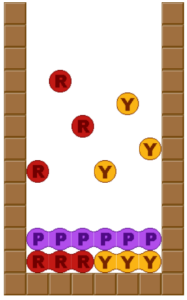
次に、これだと間に1連鎖しかなく2Wか3連鎖にしかならないので、この紫の部分の連鎖を伸ばしたい。紫は赤黄がくっつく直前の最後に消える予定なので、紫が消えるより前の方に連鎖を伸ばす。
その基本となる第二の発想がこれ。
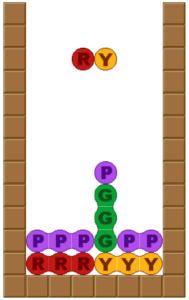
これを緑から発火すれば、緑→紫→赤黄の3Wになる。上の赤黄をずらせば4連鎖になる。
これが面白いのは、この紫を左右に割る緑はどこでも構わないところ。紫がすぐに消えないように左右に割る&頭に紫を乗せて後でくっつくようにする、という2点が達成できていればどこでも構わないので、例えば次の例はどれでも緑発火3Wになる。もちろん赤黄をずらせば4連鎖になる。ミラーも同様だ。
あとはどうにかしてこの緑より前にもう一連鎖伸ばせば4Wor5連鎖になる。これでもうどう調理しても構わない。
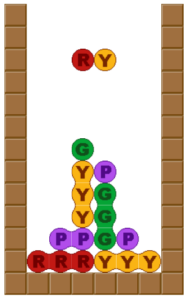
階段 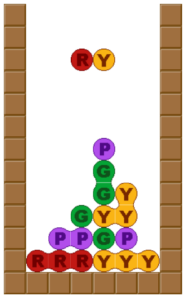
挟み込み
ぷよぷよは基本的に4色という制約がある以上色が被るので暴発しないように気を付ける必要はある。ともかくこれで4Wか5連鎖ができるようになった。めでたしめでたし。
実際に積むに当たっては当然下から順に積み上げることになるので、多少前後するにせよ基本的には下の平らな部分(上の赤黄)→板ぷよ部分(上の紫)→間の連鎖伸ばし(上の緑黄紫)→ハンバーガーの上側部分(上の赤黄)という順で作っていくことになると思われる。
考え方は習得できたのだが全然組めない。基本的な考え方は分かったが自由度が高すぎるのと、暴発しやすさからまるで上手く組み進められない。
自由度が高いということは様々な組ぷよを生かしうること、暴発しやすさは多色発火や裏発火の可能性の裏返しだとは思うのだが、ごみを捨てるのにもちょっと頭を使ってしまうのには辟易する。これは慣れの問題なのだろうか。安定的に超効率で組めたら本当にかっこいいと思うんだけどなあ。
数学III 上級問題精講をちょっとやった。受験期に買って結局全然やらずに受験を終えてしまって放っていた物体なのだが、最近数学というものに全く触れていない状態だったので久しぶりに開いてちょっと楽しくなった。
あんまり面白い数学の話をするのは得意ではないが、数式いじりは好きな方だ。
二次曲線の接線方程式がなんか元の数式と似た形になるやつ($x^2+y^2=1$の接線が$x^\prime x + y^\prime y=1$みたいに表せるやつ)を見て、そういやそんなのあったなーと思って一般化してみた。
$ax^2+by^2+cxy+dx+ey+f=0$
これを頑張って微分していい感じにえいやってすると
$ax^\prime x+by^\prime y + c\frac{xy^\prime+x^\prime y}{2}+d\frac{x+x^\prime}{2}+e\frac{y+y^\prime}{2}+f=0$
これになる。うーんc,d,eが結局キモイなー。
あと、反比例の式$xy=1$はたしか双曲線なんだよなーというのを思い出して、それを確認したりとかした。
$\left(
\begin{array}{ccc}
x \\
y
\end{array}
\right)
= \left(
\begin{array}{ccc}
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{array}
\right)
\left(
\begin{array}{ccc}
x^\prime \\
y^\prime
\end{array}
\right)$
これで45度回すと
$xy=(\frac{x^\prime}{\sqrt{2}}-\frac{y^\prime}{\sqrt{2}})(\frac{x^\prime}{\sqrt{2}}+\frac{y^\prime}{\sqrt{2}})=\frac{{x^\prime}^2}{2}-\frac{{y^\prime}^2}{2}=1$
となって確かに双曲線の式になる。焦点は$(x,y)=(2,2)$。
競プロをやってると離散の世界の話の方に多く触れるけど、なんだかんだ連続の世界の話が結構好きなんだよなあ。
Categories: 未分類