ABC263に出た。
A: やるだけ
B: 順にたどるだけ
C: DFS
D: 左側からx個をLに、右側からy個をRに置換した場合の総和最小値を求める問題。x+y>Nなる場合は考えなくてよい。
0≦i≦Nにおいて、左からi個を見た時の最適解と右からN-i個を見た時の最適解をそれぞれ足せば良さそうということになる。(ここで「左からi個を見た時の最適解」とか呼んでいるのは「左からx個を置換した場合のA1~Aiの総和最小値、ただしx≦iとする」といった話である。)それぞれ前計算する。
正直ちゃんと証明しないまま通してしまったのだが、
$dp[i]:=(左からi個を見た時の最適解)$
として
$dp[i]=\min(\sum_{k=1}^i A_k, l\times i, dp[i-1]+A_i)$
として右側も同様にしたらACした。
E: EDPC-Jと同じ感じのやつ。「自分自身」にも遷移しうるので、式を立てたあと移項して循環を無くす。式の立て方が思い出せなかったのでEDPC-Jの解説を読んだ結果、後ろから計算すべきだったことに気付いた。もっと早く気付けていればもっと早く解けていたとは思うが、こういうのは慣れなので2回目程度では仕方ないのかなーみたいな気も。似たような問題を何度も解くのはそういう意味で大事なのかもしれない。
F: 解けず。フローとかも疑ってみたが違った。解説を読んでみたところ、dp[i][j]:=(試合iにおいて選手jが勝ち上がった場合の最大)という置き方をするらしい。二分木における各ノードについての子孫ノードの数の総和は$O(n\log n)$になる。計算してみれば確かにそうだ。この知識は心の隅に留めておいた方が良さそう。
NHKの特集でモンテネグロの自然が特集されていて結構面白かった。大アドリア大陸の話とかが興味深かった。
あと本筋と関係ない部分だけどモンテネグロ人は身長が高いとか。初耳。
開発中のコメントシステムが一応動いた。
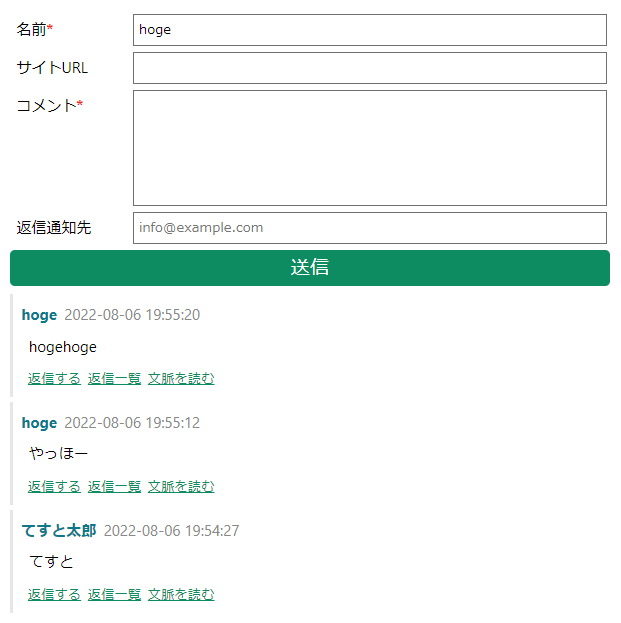
コメントの投稿・表示という最低限の動作は出来るが、予定している以下の機能はまだ実装していない。
- コメントのペジネーション (バックエンド/フロントエンド)
- 返信先を指定して送信 (フロントエンド)
- 返信があったら返信通知先にメールをポスト (バックエンド)
- 返信一覧の表示 (フロントエンド/バックエンド)
- 文脈(返信ツリー)の表示 (フロントエンド)
昼にチャーハンを作った。休日なので家族の分も作ろうとしたのだが、量を多めに作ったら水気が全く飛ばず別物になってしまった。料理は簡単にスケールしない。
Categories: 未分類