今日摂取したコンテンツ。

初手南波くんかわいい。この漫画で安心感あるのはお前しかいねえ…

対戦権利だけ渡せとかいってるコタローも大概やばいやつなんだよなあ。

女子が明らかにバキだし立ち合いは刹那の見切りだし今の小学生分からないのでは？？？？

スポンジ入れてシャキシャキにするやつは知らなかった。自分も一応昔スライム工作はしたけどこんな文化はなかった気がする。

---

今日解いた競プロの問題。

EDPC-T: トポロジカルソートのパターン数を数える問題と見なせるのには割と早く気づけた。要素を頂点、不等号を有向辺とみなすとこういう感じのグラフと見なせる。

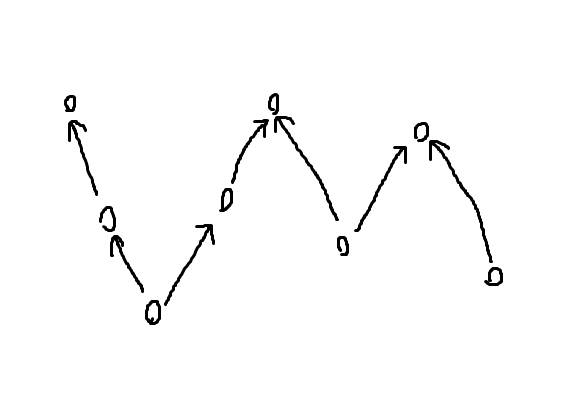
グラフを見出す能力が向上したのは嬉しい。しかしトポロジカルソートのパターン数カウントは指数時間なので、どうにかグラフの特殊性を利用して高速にカウントしなければならない。

最初は区間DPでどうにかしようと思ったが、どうあがいても$O(N^3)$から落とせず撃沈。

しかしよく考えたら、端からいくつ決めたか+最後に決めた要素の位置さえ持てば次どこに入れられるか決められることに気付く。適当に$O(N^3)$の遷移を書いた後、累積和で高速化し$O(N^2)$にしてACした。

EDPC-U: まず$O(N^2 2^N)$で1つのグループの得点を全パターン求める。それからbitDPであらゆるまとめ方に関する得点を求める。各集合について、二分割する全パターンを調べれば良い。

ある集合を2つに分けるパターンは$2^n$通りだが、各集合について$O(2^N)$かけてしまうと全体$O(2^{2N})$になってしまう。しかし各要素について「集合に含めない」「集合に含める&部分集合Aに分ける」「集合に含める&部分集合Bに分ける」という3パターンにする全探索を考えれば$O(3^N)$で求められる。3進数全探索というものがあることを覚えていて良かった。3^16は通るようだ。

3進数全探索というのはこれ。初見の時かなりビビった記憶がある。集合aは普通にbit全探索の動きをするが、集合bは集合aの全部分集合(空集合を除く)を無駄なく数え上げる。

for(int a = 0; a < (1 << n); a++)
  for(int b = a; b > 0; --b &= a)
    ...

---

昼、ふと肉料理が食べたくなって、家からしばらく歩いたデパートのレストラン街の店でサイコロステーキを頂いた。

肉…肉は全てを解決する…

---

Rustを一日書きまくっていた。慣れないのであまり開発スピードは出ないが、書いてる時の安心感がものすごい。

async/await関係はちょっと難しいな。これはRustだからではなく非同期処理が本質的に難しい。しかしコンパイルが通せないのはさすがに来るものがある。

エラーの多態性のためにいたるところでResult<(), Box<dyn Error>>みたいなコードを書いているのだが、これはあまり良くなかったりするのだろうか？エラーが一種類に絞れるなら絞った方がオーバーヘッドは少ないだろうと思うけど、どの程度良くないのかと言われると分からない。