起きたら昼だった。課題をちょっとやった。明日は趣味の進捗を出したいので、明日は出来れば午前中に課題を終わらせて午後に趣味をやれるようにしたい。
ジョギングした。2.5kmほど。
ABC282に出た。
A: 文字列作るのめんどいので1文字づつ出力した
B: O(N^2)でやるだけ、Mが30以下なのでintでビットマスク作るとよい
C: 先頭から見ていく、括られた場所かどうかのフラグを保持してダブルクォーテーションを見つけるたびに反転させるとよい
D: がんばる。各連結成分について二部グラフ判定を行い、まず二部グラフでないのが1つでも混じっていたら0。全て二部グラフだった場合、連結成分をまたいで辺を張る場合と連結成分内で辺を張る場合の二通りの辺の張り方があるのでその二つの和になる。
連結成分をまたいで辺を張る場合、これはどう張っても二部グラフ性は崩れない。連結成分の頂点数の積を足していくだけだが、nC2通りを考えるとTLEなので累積和する。
連結成分内で辺を張る場合、二部グラフとして頂点を色分けしたとして、異なる色の間でしか辺を張れない。これは各色の頂点数の積からすでに張ってある辺の数を引けばよい。これを全ての連結成分について足す。
E: グラフだと見抜けず、負け。正直グラフだと見抜けていたら解けていたかというとそれも若干怪しいが、グラフだと見抜けなかった時点でそもそもスタート地点にすら立てなかった感が強く、とても悔しい。DPでも貪欲でも筋が悪そうで、なおかつ順序に意味が無いならグラフ。心に刻む。
F: 頑張ってどのような区間が要るかを考える。あらゆる種類の区間をなるべく少ない種類の区間の和で表現する、というとセグ木構造が頭に浮かぶが、「2つの区間の和」なのでセグ木型の構造では不十分になる。
いろいろ頑張って例を考えてみた結果、こんな感じで区間を用意すれば良さそうだという結論になった。Nを2のべき乗として、区間の種類数は各段で$N$個、段数は$log_2 N \leq 12$なので50000個程度に収まる。Nが2のべき乗でない場合は[1,N]でクランプしてしまえば問題なく使える。
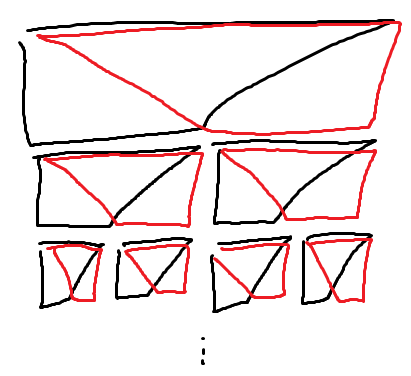
クエリに答えるくだりだが、セグ木のような良い感じの添え字構造を新たに考えだすのは明らかにだるいので、各x∈[1,N]について「$l_i$をxとする区間」「$r_i$をxとする区間」を並べ、それぞれ$r_i$と$l_i$でソートしておく。L,Rを構成する区間a,bを求められたら、「$l_i$を$L$とする区間であって$r_i$が$R$を超えないもの」「$r_i$を$R$とする区間であって$l_i$が$L$を下回らないもの」をそれぞれ二分探索で求めればよい。
ちょっと考察に時間がかかってしまったなーという気はするが、こんなのの考察を初見でそう易々と進められるか?という気がする。実はsparce tableというものの考え方らしい。
Categories: 未分類