今日解いた競プロの問題。
ARC147-C: 自力AC。ARCの青diffに少しずつ立ち向かえるようになっている…
まず、問題設定からして出来るだけ各$x_i$を近いところに集めた方が良さそうだな、というのが分かる。$x_i$を何か決めたとして、その中の最大値を下げたり最小値を上げたりすれば間違いなく不満度が下がることが簡単に証明できる。もちろん究極的には全て同じ値であることが最善である。
この問題における条件は$L_i\leq x_i \leq R_i$である。となると話は簡単で、適当な数$t$を決めて$x_i=\max(L_i, \min(R_i, t))$とすればよい。(ちゃんとした証明はしていない…)これを任意のtについて試せば不満度の最小値が求められるが、それではTLEしてしまうのでちゃんと計算する方法を考える。
今「t→不満度」という関数が構成出来たわけで、これの最小値を求めたいわけだが、なんとなくこれはU字型の関数になりそうな気がする。試してみると実際そうなっている。これに気付くのはなんか似たような問題を見てきた勘に近いので、説明が面倒くさい。
U字型の関数を最小化したい、となったら三分探索をしたくなるが、これは罠で、傾き0の領域が存在しうるので三分探索は使えない。ということで仕方なく数学的に考察してみる。不満度をtで微分した結果が0ならば極値になるだろう。傾き0の領域がどうなっているのか分からないが物は試しで。
まず$i$について、
- $R_i<t$
- $L_i\leq t \leq R_i$
- $L_i<t$
という3通りに分ける。それぞれの条件を満たす$i$の数を$A,B,C$として頑張って計算すると、詳細な計算の過程は省くが、
$\frac{d}{dt}(不満度)=B(A-C)$
であることが分かる。
これで様子が分かった。傾き0となるのはたまたま$B=0$であるような領域であり、本質は$A-C$の部分。定義から分かるように$A$は$t$に対して単調増加、$C$は$t$に対して単調減少であり、どこかしらの時点で$A-C$の符号は逆転する。このタイミングの$t$を見れば不満度の最小値がとれる。あとはもう消化試合。
各$L_i$と$R_i$を配列に詰め込んでソートし、走査していけば$A-C=0$となる$t$がとれる。この$t$で$x_i=\max(L_i, \min(R_i, t))$として不満度を計算すればよい。
最後に不満度の計算について。単純に計算すると$O(N^2)$なので高速化の必要がある。まず$x$をソートすれば絶対値記号が外せる。あとは累積和を使えば簡単に$O(N)$に高速化できる。これでこの問題が解けた。
ソートがボトルネックとなり全体$O(N\log N)$。
本質的な部分を勘と数式計算の組み合わせできっちり仕留めていけたのが良かった。終わってみるとシンプルだったので、願わくばもうちょい手早く解ければよかったなあと思わなくもない。あと、A-C=0なるtを探すところで実装を間違えて1WAした。多少ややこしいが数直線の走査は基本的な道具なので、間違わないように実装できるようにしておきたい。
なお、今日から1日1ACした問題の提出をtwitterに上げることにしてみた。なにやってんだか分かんない人に見えるので、何かしらの分かりやすい活動の印として。
筋トレをした。今日は腕立て。
新サイトのデザインを進めた。実際のページのデータを入れた方がやはりデザイン調整が捗る。
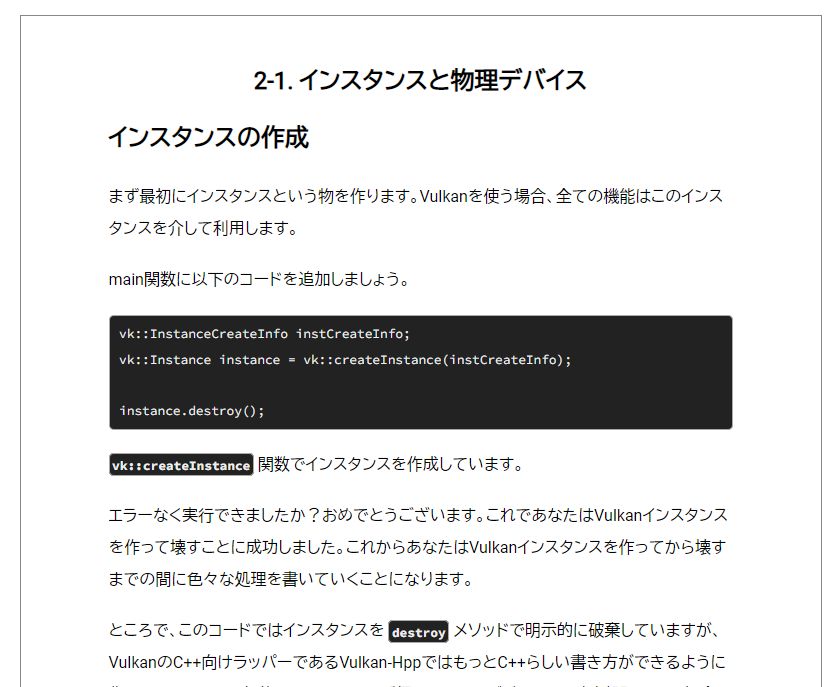
見出しなどで横幅を抑えるために英字にCondensed系のフォントを使っていたのだが、文章になるとやはり読みづらい。フォントの数が増えるのでパフォーマンス的に躊躇したが、見出しにだけCondensedフォントを使ってそれ以外を普通の英字フォントにしたらだいぶ読みやすくなった。ただやはりパフォーマンスは悪化したので、必要なページでだけ読み込むとかそういう工夫をした方が良さそう。
ソースコードの表示をどうするかで悩んだ。はみ出た場合に折り返しにするか横スクロールにするか悩んだが、githubが横スクロールにしているのでそれに倣った。横スクロールだと読むのが若干面倒という問題があるので悩んだが、折り返されたのを読むのもどっこいどっこいのUXだろう。モノクロ基調のデザインなので塗り分けも悩んだが、黒背景に白文字とした。シンタックスハイライトは重そうだし面倒そうなので却下。
サイトデザインも大詰めを迎えてきた。ヘッダーをデザインに取り入れるように方針転換したのでいくつかのページをそのように直すのと、それからパフォーマンスチューニングを終わらせれば、あとはコンテンツの中身を入れる作業に移れる。ようやくメインのサイトでWordPressを捨てられる日が来そうだ。
Categories: 未分類